Ao multiplicarmos duas raizes com o mesmo índice, podemos, pela propriedade, manter a raíz e o índice e fazer a multiplicação dentro de uma mesma raíz. Vejamos a multiplicação de algumas raizes quadradas:
O mesmo acontece para raizes com outros índices:
E como fariamos então para que a multiplicação de raizes de índice diferente de 2 nos retorne o mesmo valor do radicando, ou seja, como fazer para cancelar o índice com o expoente do radicando?
Para raizes cúbicas, precisaremos de um número elevado a 3 dentro da raíz. Portanto, precisaremos multiplicar raizes até que o radicando obtenha expoente 3. Para raizes de índice 4, precisaremos de expoente 4, e assim por diante. Veja:
Ou seja, iremos buscar uma multiplicação onde o expoente do radicando seja igual ao índice da raíz.

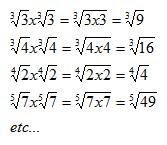



Nenhum comentário:
Postar um comentário
Observação: somente um membro deste blog pode postar um comentário.